三维曲面（3dface ）两点间在曲面距离最短的路径。

cable2004

曲面上的测地线，也就是曲面上两点间的最短路径。

[url=http://www.docin.com/p-509878812.htmlhttp://www.docin.com/p-509878812.html]
http://www.cnblogs.com/shushen/p/5174421.html

网格测地线算法（Geodesics in Heat）附源码

　　测地线又称为大地线，可以定义为空间曲面上两点的局部最短路径。测地线具有广泛的应用，例如在工业上测地线最短的性质就意味着最优最省，在航海和航空中，轮船和飞机的运行路线就是测地线。[Crane et al. 2013]提出了利用热运动方程来计算网格测地线的方法，可以想象一下，当一根烫的针尖接触到曲面上的一点时，热量会随着时间的推移而扩散，测地距离因此可以和热运动相联系。具体算法过程如下图所示：

　　第一步：热运动方程用来描述热的传播状态：

　　将热运动方程离散化并整理后得到：

其中：id为单位矩阵，t为时间间隔，Δ为离散Laplacian算子，ut为t时刻的热状态，u0为初始时刻的热状态。

　　第二步：第一步计算得到的热梯度方向与测地距离的梯度方向相同，由Eikonal方程知道测地距离的梯度为单位向量，于是通过归一化热梯度我们得到测地距离的梯度：

　　第三步：得到测地距离的梯度之后，测地线问题即变为求解以下式子：

　　根据变分法，上式最小化即求解泊松方程：

其中：Φ即为网格上顶点距离源点的测地距离。

[url=] [/url]
function [D] = geodesics_in_heat(V, F, src)       % choose time step    c = 5;    t = c * mean(doublearea(V, F))/2;    %% Step 1: Integrate the heat flow for some fixed time t    L = cotmatrix(V, F);    M = massmatrix(V, F, 'barycentric');     nV = size(V, 1);    u0 = zeros(nV, 1);    u0(src) = 1;        A = M - t*L;    B = M*u0;    nsrc = length(src);    % 1.1 dirichlet condition    hole = Cal_Boundary(F);    if isempty(hole)        boundary = [];    else        boundary = hole.boundary.edge(:,1)';    end    b = setdiff(boundary, src);    nb = [b, src];    Acons = sparse([1:length(nb)], nb, ones(1,length(nb)), length(nb), nV);    Bcons = [zeros(length(b), 1); ones(nsrc, 1)];    % 硬约束            r = setdiff([1:nV], nb);    uD = [A(r,:);Acons]\[B(r,:);Bcons];    % 1.2 neumann condition    Acons = sparse([1:nsrc], src, ones(1,nsrc), nsrc, nV);    Bcons = ones(nsrc, 1);    % 硬约束      r = setdiff([1:nV], src);    uN = [A(r,:);Acons]\[B(r,:);Bcons];        % averaged boundary condition    u = 0.5*(uN + uD);        %% Step 2: Evaluate the vector field X    G = grad(V, F); % nF*3 by nV matrix(梯度算子 - 所有三角片顶点基函数)    grad_u = reshape(G*u, size(F,1), 3); % nF by nV matrix(所有三角片中u的梯度)    grad_u_norm = sqrt(sum(grad_u.^2, 2));    normalized_grad_u = bsxfun(@rdivide, grad_u, grad_u_norm+eps);    X = -normalized_grad_u;        %% Step 3: Solve the Poisson equation    Div = div(V, F); % 散度算子    div_X = Div*X(:); % #nV by #nF*3    Lcons = sparse([1:nsrc], src, ones(1,nsrc), nsrc, nV);    div_Xcons = zeros(nsrc, 1);    % 硬约束    r = setdiff([1:nV], src);    D = [L(r,:);Lcons]\[div_X(r,:);div_Xcons];        D = D - min(D);end[url=] [/url]

效果：

本文为原创，转载请注明出处：http://www.cnblogs.com/shushen。

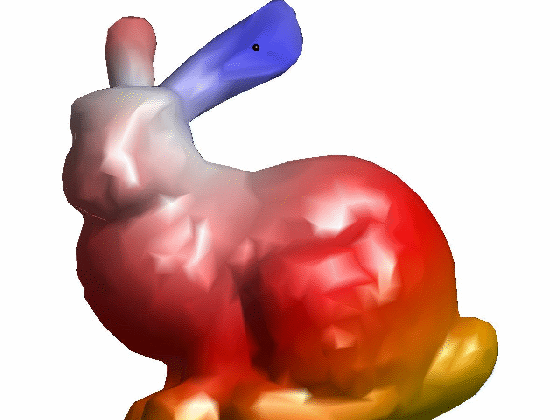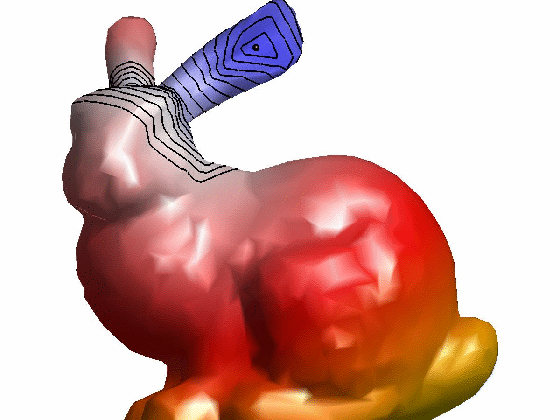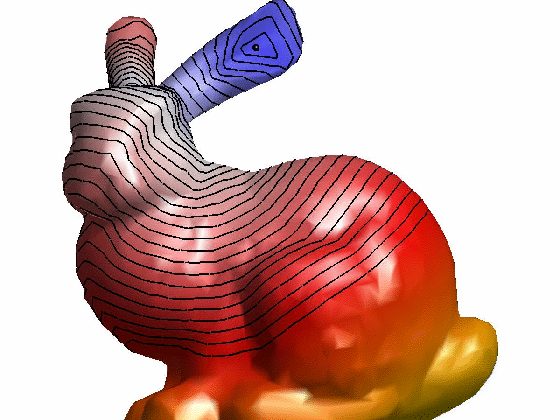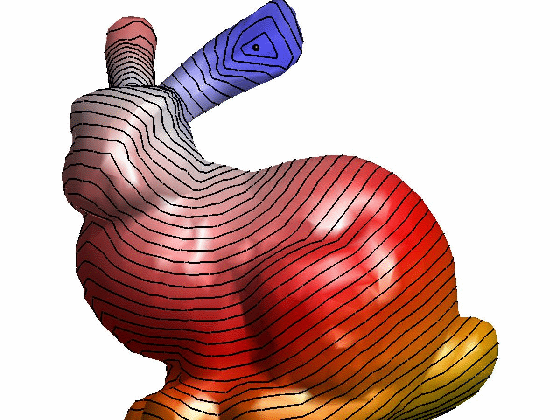
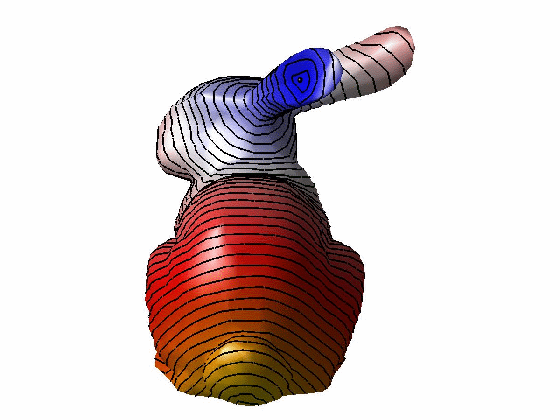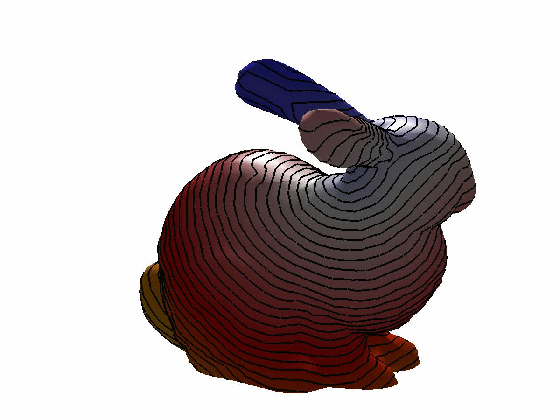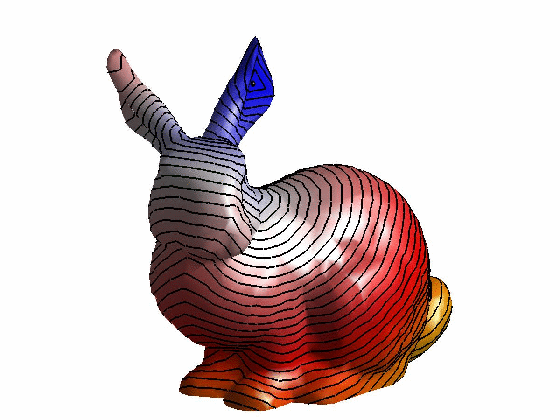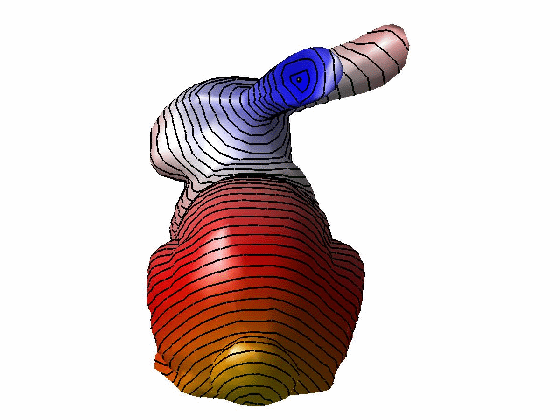
参考文献：

[1] Keenan Crane, Clarisse Weischedel, and Max Wardetzky. 2013. Geodesics in heat: A new approach to computing distance based on heat flow. ACM Trans. Graph. 32, 5, Article 152 (October 2013), 11 pages.