About Nonuniform Rational B-Splines - NURBS

XDSoft

About Nonuniform Rational B-Splines - NURBS a summary by Markus Altmann
NURBS are industry standard tools for the representation and design of geometry [ROGERS]. Some reasons for the use of NURBS are, that they: [PIEGL][ROGERS]

• offer one common mathematical form for both, standard analytical shapes (e.g. conics) and free form shapes;
• provide the flexibility to design a large variety of shapes;
• can be evaluated reasonably fast by numerically stable and accurate algorithms;
• are invariant under affine as well as perspective transformations;
• are generalizations of non-rational B-splines and non-rational and rational Bezier curves and surfaces.
  

However, one of the drawbacks NURBS have, is the need for extra storage to define traditional shapes (e.g. circles). This results from parameters in addition to the control points, but finally allow the desired flexibility for defining parametric shapes. NURBS-shapes are not only defined by control points; weights, associated with each control point are also necessary. A NURBS curve C(u), for examples, which is a vector-valued piecewise rational polynomial function, is defined as: [PIEGL]
                sum(i = 0, n){w_i * P_i * N_i,k(u)}        C(u) = -------------------------------------,         (1)                     sum(i = 0, n){w_i * N_i,k(u)}where
        w_i : weights        P_i : control points (vector)        N_i,k : normalized B-spline basis functions of degree kThese B-splines are defined recursively as:

                u - t_i   N_i,k(u) = ----------- * N_i,k-1(u) +              t_i+k - t_i                t_i+k+1 - u              ---------------  * N_i+1,k-1(u)        (2)              t_i+k+1 - t_i+1and
                    / 1, if t_i <= u < t_i+1        N_i,0(u) = <                    \ 0, elsewhere t_i are the knots forming a knot vector

        U = { t_0, t_1, ... , t_m }.

The Knot Vector

The knot vector uniquely determines the B-splines as it is obvious from (2). The relation between the number of knots (m+1), the degree (k) of N_i,k and the number of control points (n+1) is given by m = n + k + 1 [PEIGL][ROGERS].The sequence of knots in the knot vector U is assumed to be nondecreasing, i.e. t_i <= t_i+1. Each successive pair of knots represents an interval [t_i, t_i+1) for the parameter values to calculate a segment of a shape [FOLEY][WATT].
For NURBS, the relative parametric intervals (knot spans) need not be the same for all shape segments, i.e. the knot spacing is nonuniform, leading to a non-periodic knot vector of the form

   U = { a, ... , a, t_k+1, ... , t_m-k-1, b, ... , b },   (3)where a and b are repeated with multiplicity of k+1 [ROGERS][PIEGL]. The multiplicity of a knot affects the parametric continuity at this knot [FOLEY]. Non-periodic B-splines, like NURBS, are infinitely continuously differentiable in the interior of a knot span and k-M-1 times continuously differentiable at a knot, where M is the multiplicity of the knot [ROGERS]. (In contrast, a periodic knot vector U = { 0, 1, ... , n } is everywhere k-1 times continuously differentiable.) Considering the knot vector for NURBS, the end knot points (t_k, t_n+1) with multiplicity k+1 coincide with the end control points P_0, P_n.
Since the knot spacing could be nonuniform, the B-splines are no longer the same for each interval [t_i, t_i+1) and the degree of the B-Spline can vary [WATT][FOLEY]. Considering the whole range of parameter values represented by the knot vector, the different B-splines build up continuous (overlapping) blending functions N_i,k(u), as defined in (2), over this range (Fig. 1) [WATT]. These blending functions have the following properties: [WATT][ROGERS]

• N_i,k(u) >= 0, for all i, k, u;
• N_i,k(u) = 0, if u not in [t_i, t_i+k+1), meaning local support of k+1 knot spans, where N_i,k(u) is nonzero;
• if u in [t_i, t_i+1), the non-vanishing blending functions are N_i-k,k(u), ..., N_i,k(u)
• sum(j=i-k, i){N_j,k(u)} = sum(i=0, n){N_i,k(u)} = 1, (partition of unity)
• in case of multiple knots, 0/0 is deemed to be zero.
  

1. and 4. together result into the convex hull, the control points build up for a shape defined by NURBS [WATT]. 2. and 3. show, that k+1 successive control points define a shape segment, and a control point is involved in k+1 neighboring shape segments. Therefore, changing a control point or weight influences just k+1 shape segments, defined over the interval given in 2.

Curve/Surface Definition

The previous definition of a NURBS-curve (1) can be rewritten using rational basis functions [PEIGL][ROGERS][WATT]
                          w_i * N_i,k(u)        R_i,k(u) = ----------------------------                   sum(j = 0, n){w_j * N_j,k(u)}into        C(u) = sum(i = 0, n){P_i * R_i,k(u)

}.
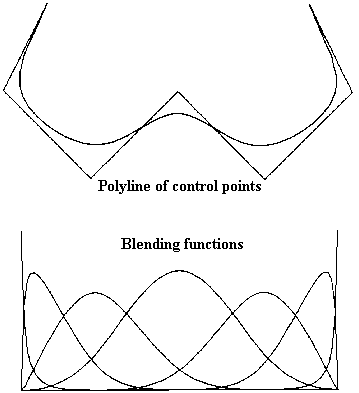
Fig. 1: Cubic NURBS curve with associated blending functions.A NURBS-surface is define in a similar way:

    S(u, v) = sum(i = 0, n)sum(j = 0, m) P_i,j * R_i,k, j,l(u, v) ,where                                 w_i,j * N_i,k(u) * N_j,l(v)R_i,k,j,l(u, v) = ---------------------------------------------------------                  sum(r = 0, n){sum(s = 0, m){w_r,s * N_r,k(u) * N_s,l(u)}}The rational basis functions have the same properties as the blending functions [PEIGL][ROGERS]. One point to emphasize, is their invariance under affine and (even) perspective transformations. Therefore, only the control points have to be transformed to get the appropriate transformation of the NURBS shape.

Computational Algorithm

NURBS can be evaluated effectively by using homogeneous coordinates [PEIGL][ROGERS]. The following steps perform the evaluation:

• add one dimension to the control points (e.g. P = (x, y) -> P'(x, y, 1)) and multiply them by their corresponding weights, i.e. in 2D: P_i(x_i, y_i) -> P_i'(w_i * x_i, w_i * y_i, w_i)
• calculate NURBS in homogeneous coordinates:
     C'(u) = sum(i = 0, n){P_i'(u) * N_i,k(u)}
• map "homogeneous" NURBS back to original coordinate system with:
  

                             / ( X1/W, X2/W, ... , Xn/W ), if W not = 0 map( X1, X2, ... ,Xn, W) = <                             \ ( X1, X2, ... , Xn ), if W = 0                         sum(i = 0, n){w_i * P_i * N_i,k(u)}   C(u) = map( C'(u) ) = -----------------------------------                            sum(i = 0, n){w_i * N_i,k(u)}For u in [t_i, t_i+1), the only existing blending functions to consider in evaluation of the curve at u are N_i-k,k(u), ..., N_i,k(u). An effective algorithm for the computation of the non-vanishing blending functions exists in [deBOOR pp. 132 - 135].


The Weights

As mentioned above, changing the weight w_i of a control point P_i affects only the range [t_i, t_i+k+1) (in case of a curve). The geometric meaning of the weights is shown as follows (Fig. 2) [PEIGL][ROGERS].Defining the points:

                B = C(u; w_i = 0)                N = C(u; w_i = 1)                B_i = C(u; w_i not = {0, 1})


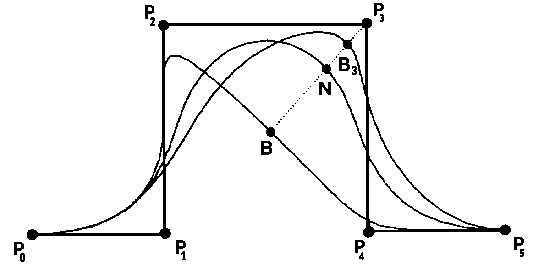
Fig. 2:

Geometric meaning of weights (w_3).
N and B_i can also be expressed as:

                N = (1 - a) * B + a * P_i                B_i = (1 - b) * B + b * P_i ,where                a = R_i,k(u; w_i = 1)                b = R_i,k(u).The following identity is obtained from the expression of a and b:

        (1 - a)/a : (1 - b)/b = P_iN/BN : P_iB_i/BB_i = w_i ,which is called the cross- or double ratio of the four points P_i, B, N, B_i. From these expressions, the effect of shape modification can be derived:

• B_i sweeps out on a straight line segment
• if w_i = 0 then P_i has no effect on shape
• if w_i increases, so b and the curve is pulled toward P_i and pushed away from P_j, for j not= i
• if w_i decreases, so b and the curve is pushed away from P_i and pulled toward P_j, for j not= i
• if w_i -> infinity then b -> 1 and B_i -> P_i, if u in [t_i, t_i+k+1)
  

---

References:
[deBOOR] C. deBoor,
"A Practical Guide to Splines",
1978, New York, Springer-Verlag
[FOLEY] James D. Foley et al.,
"Introduction to Computer Graphics",
1994, Addision-Wesley
[PEIGL] Les Piegl
"On NURBS: A Survey",
Jan 01, 1991, IEEE Computer Graphics and Applications, Vol. 11, No. 1, pp. 55 - 71
[ROGERS] David F. Rogers, Rae A. Earnshaw (editors),
"State of the Art in Computer Graphics - Visualization and Modeling",
1991, New York, Springer-Verlag, pp. 225 - 269
[WATT] Alan Watt, Mark Watt,
"Advanced Animation and Rendering Techniques",
1992, New York, AMC press, Addision-Wesley