马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?立即注册


×
对平面上的一些点拟合有很多手段,其中椭圆拟合在图像轮廓划分等很多方面都很重要,当然,我们一般还是用最小二乘法来拟合椭圆, 在这里,我实现了两种算法,一种是
[html] view plaincopy
- http://wenku.baidu.com/link?url=7kIrC8LoOMCtlmAH8yqkpUQfiKwWnVe4EoUJekkQSgQ1qTWfLAuEXTYvYTv7SATGIJYX4IxcTIB94-iO0SpUgztWgx661O2VEOwm_dvoSqO
这篇文章给出的,核心也是最小二乘法,利用gauss消去法解方程组,不过他给出的代码有些小bug,所以我改了一下,也去掉了opencv的东西。
还有一个就是利用奇异值分解法来求超定方程的最小二乘法的思想来求出椭圆的五个参数,关于奇异值分解法可以参考 http://blog.csdn.net/wangzhiqing3/article/details/7446444 下面是我的代码实现:
//LSEllipse.h
[cpp] view plaincopy
- /*************************************************************************
- 版本: 2014-12-31
- 功能说明: 对平面上的一些列点给出最小二乘的椭圆拟合,利用奇异值分解法
- 解得最小二乘解作为椭圆参数。
- 调用形式: cvFitEllipse2f(arrayx,arrayy,box);
- 参数说明: arrayx: arrayx[n],每个值为x轴一个点
- arrayx: arrayy[n],每个值为y轴一个点
- n : 点的个数
- box : box[5],椭圆的五个参数,分别为center.x,center.y,2a,2b,xtheta
- esp: 解精度,通常取1e-6,这个是解方程用的说
- ***************************************************************************/
-
-
-
-
- #include"stdafx.h"
- #include<cstdlib>
- #include<float.h>
- #include<vector>
- using namespace std;
-
- class LSEllipse
- {
- public:
- LSEllipse(void);
- ~LSEllipse(void);
- vector<double> getEllipseparGauss(vector<CPoint> vec_point);
- void cvFitEllipse2f( int *arrayx, int *arrayy,int n,float *box );
- private:
- int SVD(float *a,int m,int n,float b[],float x[],float esp);
- int gmiv(float a[],int m,int n,float b[],float x[],float aa[],float eps,float u[],float v[],int ka);
- int ginv(float a[],int m,int n,float aa[],float eps,float u[],float v[],int ka);
- int muav(float a[],int m,int n,float u[],float v[],float eps,int ka);
- };
//LSEllipse.cpp
[cpp] view plaincopy
- #include"stdafx.h"
- #include "LSEllipse.h"
- #include <cmath>
-
- LSEllipse::LSEllipse(void)
- {
- }
-
-
- LSEllipse::~LSEllipse(void)
- {
- }
- //列主元高斯消去法
- //A为系数矩阵,x为解向量,若成功,返回true,否则返回false,并将x清空。
-
- bool RGauss(const vector<vector<double> > & A, vector<double> & x)
- {
- x.clear();
- int n = A.size();
- int m = A[0].size();
- x.resize(n);
- //复制系数矩阵,防止修改原矩阵
- vector<vector<double> > Atemp(n);
- for (int i = 0; i < n; i++)
- {
- vector<double> temp(m);
- for (int j = 0; j < m; j++)
- {
- temp[j] = A[j];
- }
- Atemp = temp;
- temp.clear();
- }
- for (int k = 0; k < n; k++)
- {
- //选主元
- double max = -1;
- int l = -1;
- for (int i = k; i < n; i++)
- {
- if (abs(Atemp[k]) > max)
- {
- max = abs(Atemp[k]);
- l = i;
- }
- }
- if (l != k)
- {
- //交换系数矩阵的l行和k行
- for (int i = 0; i < m; i++)
- {
- double temp = Atemp[l];
- Atemp[l] = Atemp[k];
- Atemp[k] = temp;
- }
- }
- //消元
- for (int i = k+1; i < n; i++)
- {
- double l = Atemp[k]/Atemp[k][k];
- for (int j = k; j < m; j++)
- {
- Atemp[j] = Atemp[j] - l*Atemp[k][j];
- }
- }
- }
- //回代
- x[n-1] = Atemp[n-1][m-1]/Atemp[n-1][m-2];
- for (int k = n-2; k >= 0; k--)
- {
- double s = 0.0;
- for (int j = k+1; j < n; j++)
- {
- s += Atemp[k][j]*x[j];
- }
- x[k] = (Atemp[k][m-1] - s)/Atemp[k][k];
- }
- return true;
- }
-
- vector<double> LSEllipse::getEllipseparGauss(vector<CPoint> vec_point)
- {
- vector<double> vec_result;
- double x3y1 = 0,x1y3= 0,x2y2= 0,yyy4= 0, xxx3= 0,xxx2= 0,x2y1= 0,yyy3= 0,x1y2= 0 ,yyy2= 0,x1y1= 0,xxx1= 0,yyy1= 0;
- int N = vec_point.size();
- for (int m_i = 0;m_i < N ;++m_i )
- {
- double xi = vec_point[m_i].x ;
- double yi = vec_point[m_i].y;
- x3y1 += xi*xi*xi*yi ;
- x1y3 += xi*yi*yi*yi;
- x2y2 += xi*xi*yi*yi; ;
- yyy4 +=yi*yi*yi*yi;
- xxx3 += xi*xi*xi ;
- xxx2 += xi*xi ;
- x2y1 += xi*xi*yi;
-
- x1y2 += xi*yi*yi;
- yyy2 += yi*yi;
- x1y1 += xi*yi;
- xxx1 += xi;
- yyy1 += yi;
- yyy3 += yi*yi*yi;
- }
- double resul[5];
- resul[0] = -(x3y1);
- resul[1] = -(x2y2);
- resul[2] = -(xxx3);
- resul[3] = -(x2y1);
- resul[4] = -(xxx2);
- long double Bb[5],Cc[5],Dd[5],Ee[5],Aa[5];
- Bb[0] = x1y3, Cc[0] = x2y1, Dd[0] = x1y2, Ee[0] = x1y1, Aa[0] = x2y2;
- Bb[1] = yyy4, Cc[1] = x1y2, Dd[1] = yyy3, Ee[1] = yyy2, Aa[1] = x1y3;
- Bb[2] = x1y2, Cc[2] = xxx2, Dd[2] = x1y1, Ee[2] = xxx1, Aa[2] = x2y1;
- Bb[3] = yyy3, Cc[3]= x1y1, Dd[3] = yyy2, Ee[3] = yyy1, Aa[3] = x1y2;
- Bb[4]= yyy2, Cc[4]= xxx1, Dd[4] = yyy1, Ee[4] = N, Aa[4]= x1y1;
-
- vector<vector<double>>Ma(5);
- vector<double>Md(5);
- for(int i=0;i<5;i++)
- {
- Ma.push_back(Aa);
- Ma.push_back(Bb);
- Ma.push_back(Cc);
- Ma.push_back(Dd);
- Ma.push_back(Ee);
- Ma.push_back(resul);
- }
-
- RGauss(Ma,Md);
- long double A=Md[0];
- long double B=Md[1];
- long double C=Md[2];
- long double D=Md[3];
- long double E=Md[4];
- double XC=(2*B*C-A*D)/(A*A-4*B);
- double YC=(2*D-A*C)/(A*A-4*B);
- long double fenzi=2*(A*C*D-B*C*C-D*D+4*E*B-A*A*E);
- long double fenmu=(A*A-4*B)*(B-sqrt(A*A+(1-B)*(1-B))+1);
- long double fenmu2=(A*A-4*B)*(B+sqrt(A*A+(1-B)*(1-B))+1);
- double XA=sqrt(fabs(fenzi/fenmu));
- double XB=sqrt(fabs(fenzi/fenmu2));
- double Xtheta=0.5*atan(A/(1-B))*180/3.1415926;
- if(B<1)
- Xtheta+=90;
- vec_result.push_back(XC);
- vec_result.push_back(YC);
- vec_result.push_back(XA);
- vec_result.push_back(XB);
- vec_result.push_back(Xtheta);
- return vec_result;
- }
-
- void LSEllipse::cvFitEllipse2f( int *arrayx, int *arrayy,int n,float *box )
- {
- float cx=0,cy=0;
- double rp[5], t;
- float *A1=new float[n*5];
- float *A2=new float[2*2];
- float *A3=new float[n*3];
- float *B1=new float[n],*B2=new float[2],*B3=new float[n];
- const double min_eps = 1e-6;
- int i;
- for( i = 0; i < n; i++ )
- {
-
- cx += arrayx*1.0;
- cy += arrayy*1.0;
-
- }
- cx /= n;
- cy /= n;
- for( i = 0; i < n; i++ )
- {
- int step=i*5;
- float px,py;
- px = arrayx*1.0;
- py = arrayy*1.0;
- px -= cx;
- py -= cy;
- B1 = 10000.0;
- A1[step] = -px * px;
- A1[step + 1] = -py * py;
- A1[step + 2] = -px * py;
- A1[step + 3] = px;
- A1[step + 4] = py;
- }
- float *x1=new float[5];
- //解出Ax^2+By^2+Cxy+Dx+Ey=10000的最小二乘解!
- SVD(A1,n,5,B1,x1,min_eps);
- A2[0]=2*x1[0],A2[1]=A2[2]=x1[2],A2[3]=2*x1[1];
- B2[0]=x1[3],B2[1]=x1[4];
- float *x2=new float[2];
- //标准化,将一次项消掉,求出center.x和center.y;
- SVD(A2,2,2,B2,x2,min_eps);
- rp[0]=x2[0],rp[1]=x2[1];
- for( i = 0; i < n; i++ )
- {
- float px,py;
- px = arrayx*1.0;
- py = arrayy*1.0;
- px -= cx;
- py -= cy;
- B3 = 1.0;
- int step=i*3;
- A3[step] = (px - rp[0]) * (px - rp[0]);
- A3[step+1] = (py - rp[1]) * (py - rp[1]);
- A3[step+2] = (px - rp[0]) * (py - rp[1]);
-
- }
- //求出A(x-center.x)^2+B(y-center.y)^2+C(x-center.x)(y-center.y)的最小二乘解
- SVD(A3,n,3,B3,x1,min_eps);
-
- rp[4] = -0.5 * atan2(x1[2], x1[1] - x1[0]);
- t = sin(-2.0 * rp[4]);
- if( fabs(t) > fabs(x1[2])*min_eps )
- t = x1[2]/t;
- else
- t = x1[1] - x1[0];
- rp[2] = fabs(x1[0] + x1[1] - t);
- if( rp[2] > min_eps )
- rp[2] = sqrt(2.0 / rp[2]);
- rp[3] = fabs(x1[0] + x1[1] + t);
- if( rp[3] > min_eps )
- rp[3] = sqrt(2.0 / rp[3]);
-
- box[0] = (float)rp[0] + cx;
- box[1]= (float)rp[1] + cy;
- box[2]= (float)(rp[2]*2);
- box[3] = (float)(rp[3]*2);
- if( box[2] > box[3] )
- {
- double tmp=box[2];
- box[2]=box[3];
- box[3]=tmp;
- }
- box[4] = (float)(90 + rp[4]*180/3.1415926);
- if( box[4] < -180 )
- box[4] += 360;
- if( box[4] > 360 )
- box[4] -= 360;
- delete []A1;
- delete []A2;
- delete []A3;
- delete []B1;
- delete []B2;
- delete []B3;
- delete []x1;
- delete []x2;
-
- }
-
- int LSEllipse::SVD(float *a,int m,int n,float b[],float x[],float esp)
- {
- float *aa;
- float *u;
- float *v;
- aa=new float[n*m];
- u=new float[m*m];
- v=new float[n*n];
-
- int ka;
- int flag;
- if(m>n)
- {
- ka=m+1;
- }else
- {
- ka=n+1;
- }
-
- flag=gmiv(a,m,n,b,x,aa,esp,u,v,ka);
-
-
-
- delete []aa;
- delete []u;
- delete []v;
-
- return(flag);
- }
-
-
-
-
-
- int LSEllipse::gmiv( float a[],int m,int n,float b[],float x[],float aa[],float eps,float u[],float v[],int ka)
- {
- int i,j;
- i=ginv(a,m,n,aa,eps,u,v,ka);
-
- if (i<0) return(-1);
- for (i=0; i<=n-1; i++)
- { x=0.0;
- for (j=0; j<=m-1; j++)
- x=x+aa[i*m+j]*b[j];
- }
- return(1);
- }
-
-
- int LSEllipse::ginv(float a[],int m,int n,float aa[],float eps,float u[],float v[],int ka)
- {
-
- // int muav(float a[],int m,int n,float u[],float v[],float eps,int ka);
-
- int i,j,k,l,t,p,q,f;
- i=muav(a,m,n,u,v,eps,ka);
- if (i<0) return(-1);
- j=n;
- if (m<n) j=m;
- j=j-1;
- k=0;
- while ((k<=j)&&(a[k*n+k]!=0.0)) k=k+1;
- k=k-1;
- for (i=0; i<=n-1; i++)
- for (j=0; j<=m-1; j++)
- { t=i*m+j; aa[t]=0.0;
- for (l=0; l<=k; l++)
- { f=l*n+i; p=j*m+l; q=l*n+l;
- aa[t]=aa[t]+v[f]*u[p]/a[q];
- }
- }
- return(1);
- }
-
-
-
-
-
-
- int LSEllipse::muav(float a[],int m,int n,float u[],float v[],float eps,int ka)
- { int i,j,k,l,it,ll,kk,ix,iy,mm,nn,iz,m1,ks;
- float d,dd,t,sm,sm1,em1,sk,ek,b,c,shh,fg[2],cs[2];
- float *s,*e,*w;
- //void ppp();
- // void sss();
- void ppp(float a[],float e[],float s[],float v[],int m,int n);
- void sss(float fg[],float cs[]);
-
- s=(float *) malloc(ka*sizeof(float));
- e=(float *) malloc(ka*sizeof(float));
- w=(float *) malloc(ka*sizeof(float));
- it=60; k=n;
- if (m-1<n) k=m-1;
- l=m;
- if (n-2<m) l=n-2;
- if (l<0) l=0;
- ll=k;
- if (l>k) ll=l;
- if (ll>=1)
- { for (kk=1; kk<=ll; kk++)
- { if (kk<=k)
- { d=0.0;
- for (i=kk; i<=m; i++)
- { ix=(i-1)*n+kk-1; d=d+a[ix]*a[ix];}
- s[kk-1]=(float)sqrt(d);
- if (s[kk-1]!=0.0)
- { ix=(kk-1)*n+kk-1;
- if (a[ix]!=0.0)
- { s[kk-1]=(float)fabs(s[kk-1]);
- if (a[ix]<0.0) s[kk-1]=-s[kk-1];
- }
- for (i=kk; i<=m; i++)
- { iy=(i-1)*n+kk-1;
- a[iy]=a[iy]/s[kk-1];
- }
- a[ix]=1.0f+a[ix];
- }
- s[kk-1]=-s[kk-1];
- }
- if (n>=kk+1)
- { for (j=kk+1; j<=n; j++)
- { if ((kk<=k)&&(s[kk-1]!=0.0))
- { d=0.0;
- for (i=kk; i<=m; i++)
- { ix=(i-1)*n+kk-1;
- iy=(i-1)*n+j-1;
- d=d+a[ix]*a[iy];
- }
- d=-d/a[(kk-1)*n+kk-1];
- for (i=kk; i<=m; i++)
- { ix=(i-1)*n+j-1;
- iy=(i-1)*n+kk-1;
- a[ix]=a[ix]+d*a[iy];
- }
- }
- e[j-1]=a[(kk-1)*n+j-1];
- }
- }
- if (kk<=k)
- { for (i=kk; i<=m; i++)
- { ix=(i-1)*m+kk-1; iy=(i-1)*n+kk-1;
- u[ix]=a[iy];
- }
- }
- if (kk<=l)
- { d=0.0;
- for (i=kk+1; i<=n; i++)
- d=d+e[i-1]*e[i-1];
- e[kk-1]=(float)sqrt(d);
- if (e[kk-1]!=0.0)
- { if (e[kk]!=0.0)
- { e[kk-1]=(float)fabs(e[kk-1]);
- if (e[kk]<0.0) e[kk-1]=-e[kk-1];
- }
- for (i=kk+1; i<=n; i++)
- e[i-1]=e[i-1]/e[kk-1];
- e[kk]=1.0f+e[kk];
- }
- e[kk-1]=-e[kk-1];
- if ((kk+1<=m)&&(e[kk-1]!=0.0))
- { for (i=kk+1; i<=m; i++) w[i-1]=0.0;
- for (j=kk+1; j<=n; j++)
- for (i=kk+1; i<=m; i++)
- w[i-1]=w[i-1]+e[j-1]*a[(i-1)*n+j-1];
- for (j=kk+1; j<=n; j++)
- for (i=kk+1; i<=m; i++)
- { ix=(i-1)*n+j-1;
- a[ix]=a[ix]-w[i-1]*e[j-1]/e[kk];
- }
- }
- for (i=kk+1; i<=n; i++)
- v[(i-1)*n+kk-1]=e[i-1];
- }
- }
- }
- mm=n;
- if (m+1<n) mm=m+1;
- if (k<n) s[k]=a[k*n+k];
- if (m<mm) s[mm-1]=0.0;
- if (l+1<mm) e[l]=a[l*n+mm-1];
- e[mm-1]=0.0;
- nn=m;
- if (m>n) nn=n;
- if (nn>=k+1)
- { for (j=k+1; j<=nn; j++)
- { for (i=1; i<=m; i++)
- u[(i-1)*m+j-1]=0.0;
- u[(j-1)*m+j-1]=1.0;
- }
- }
- if (k>=1)
- { for (ll=1; ll<=k; ll++)
- { kk=k-ll+1; iz=(kk-1)*m+kk-1;
- if (s[kk-1]!=0.0)
- { if (nn>=kk+1)
- for (j=kk+1; j<=nn; j++)
- { d=0.0;
- for (i=kk; i<=m; i++)
- { ix=(i-1)*m+kk-1;
- iy=(i-1)*m+j-1;
- d=d+u[ix]*u[iy]/u[iz];
- }
- d=-d;
- for (i=kk; i<=m; i++)
- { ix=(i-1)*m+j-1;
- iy=(i-1)*m+kk-1;
- u[ix]=u[ix]+d*u[iy];
- }
- }
- for (i=kk; i<=m; i++)
- { ix=(i-1)*m+kk-1; u[ix]=-u[ix];}
- u[iz]=1.0f+u[iz];
- if (kk-1>=1)
- for (i=1; i<=kk-1; i++)
- u[(i-1)*m+kk-1]=0.0;
- }
- else
- { for (i=1; i<=m; i++)
- u[(i-1)*m+kk-1]=0.0;
- u[(kk-1)*m+kk-1]=1.0;
- }
- }
- }
- for (ll=1; ll<=n; ll++)
- { kk=n-ll+1; iz=kk*n+kk-1;
- if ((kk<=l)&&(e[kk-1]!=0.0))
- { for (j=kk+1; j<=n; j++)
- { d=0.0;
- for (i=kk+1; i<=n; i++)
- { ix=(i-1)*n+kk-1; iy=(i-1)*n+j-1;
- d=d+v[ix]*v[iy]/v[iz];
- }
- d=-d;
- for (i=kk+1; i<=n; i++)
- { ix=(i-1)*n+j-1; iy=(i-1)*n+kk-1;
- v[ix]=v[ix]+d*v[iy];
- }
- }
- }
- for (i=1; i<=n; i++)
- v[(i-1)*n+kk-1]=0.0;
- v[iz-n]=1.0;
- }
- for (i=1; i<=m; i++)
- for (j=1; j<=n; j++)
- a[(i-1)*n+j-1]=0.0;
- m1=mm; it=60;
- while (1==1)
- { if (mm==0)
- { ppp(a,e,s,v,m,n);
- free(s); free(e); free(w); return(1);
- }
- if (it==0)
- { ppp(a,e,s,v,m,n);
- free(s); free(e); free(w); return(-1);
- }
- kk=mm-1;
- while ((kk!=0)&&(fabs(e[kk-1])!=0.0))
- { d=(float)(fabs(s[kk-1])+fabs(s[kk]));
- dd=(float)fabs(e[kk-1]);
- if (dd>eps*d) kk=kk-1;
- else e[kk-1]=0.0;
- }
- if (kk==mm-1)
- { kk=kk+1;
- if (s[kk-1]<0.0)
- { s[kk-1]=-s[kk-1];
- for (i=1; i<=n; i++)
- { ix=(i-1)*n+kk-1; v[ix]=-v[ix];}
- }
- while ((kk!=m1)&&(s[kk-1]<s[kk]))
- { d=s[kk-1]; s[kk-1]=s[kk]; s[kk]=d;
- if (kk<n)
- for (i=1; i<=n; i++)
- { ix=(i-1)*n+kk-1; iy=(i-1)*n+kk;
- d=v[ix]; v[ix]=v[iy]; v[iy]=d;
- }
- if (kk<m)
- for (i=1; i<=m; i++)
- { ix=(i-1)*m+kk-1; iy=(i-1)*m+kk;
- d=u[ix]; u[ix]=u[iy]; u[iy]=d;
- }
- kk=kk+1;
- }
- it=60;
- mm=mm-1;
- }
- else
- { ks=mm;
- while ((ks>kk)&&(fabs(s[ks-1])!=0.0))
- { d=0.0;
- if (ks!=mm) d=d+(float)fabs(e[ks-1]);
- if (ks!=kk+1) d=d+(float)fabs(e[ks-2]);
- dd=(float)fabs(s[ks-1]);
- if (dd>eps*d) ks=ks-1;
- else s[ks-1]=0.0;
- }
- if (ks==kk)
- { kk=kk+1;
- d=(float)fabs(s[mm-1]);
- t=(float)fabs(s[mm-2]);
- if (t>d) d=t;
- t=(float)fabs(e[mm-2]);
- if (t>d) d=t;
- t=(float)fabs(s[kk-1]);
- if (t>d) d=t;
- t=(float)fabs(e[kk-1]);
- if (t>d) d=t;
- sm=s[mm-1]/d; sm1=s[mm-2]/d;
- em1=e[mm-2]/d;
- sk=s[kk-1]/d; ek=e[kk-1]/d;
- b=((sm1+sm)*(sm1-sm)+em1*em1)/2.0f;
- c=sm*em1; c=c*c; shh=0.0;
- if ((b!=0.0)||(c!=0.0))
- { shh=(float)sqrt(b*b+c);
- if (b<0.0) shh=-shh;
- shh=c/(b+shh);
- }
- fg[0]=(sk+sm)*(sk-sm)-shh;
- fg[1]=sk*ek;
- for (i=kk; i<=mm-1; i++)
- { sss(fg,cs);
- if (i!=kk) e[i-2]=fg[0];
- fg[0]=cs[0]*s[i-1]+cs[1]*e[i-1];
- e[i-1]=cs[0]*e[i-1]-cs[1]*s[i-1];
- fg[1]=cs[1]*s;
- s=cs[0]*s;
- if ((cs[0]!=1.0)||(cs[1]!=0.0))
- for (j=1; j<=n; j++)
- { ix=(j-1)*n+i-1;
- iy=(j-1)*n+i;
- d=cs[0]*v[ix]+cs[1]*v[iy];
- v[iy]=-cs[1]*v[ix]+cs[0]*v[iy];
- v[ix]=d;
- }
- sss(fg,cs);
- s[i-1]=fg[0];
- fg[0]=cs[0]*e[i-1]+cs[1]*s;
- s=-cs[1]*e[i-1]+cs[0]*s;
- fg[1]=cs[1]*e;
- e=cs[0]*e;
- if (i<m)
- if ((cs[0]!=1.0)||(cs[1]!=0.0))
- for (j=1; j<=m; j++)
- { ix=(j-1)*m+i-1;
- iy=(j-1)*m+i;
- d=cs[0]*u[ix]+cs[1]*u[iy];
- u[iy]=-cs[1]*u[ix]+cs[0]*u[iy];
- u[ix]=d;
- }
- }
- e[mm-2]=fg[0];
- it=it-1;
- }
- else
- { if (ks==mm)
- { kk=kk+1;
- fg[1]=e[mm-2]; e[mm-2]=0.0;
- for (ll=kk; ll<=mm-1; ll++)
- { i=mm+kk-ll-1;
- fg[0]=s[i-1];
- sss(fg,cs);
- s[i-1]=fg[0];
- if (i!=kk)
- { fg[1]=-cs[1]*e[i-2];
- e[i-2]=cs[0]*e[i-2];
- }
- if ((cs[0]!=1.0)||(cs[1]!=0.0))
- for (j=1; j<=n; j++)
- { ix=(j-1)*n+i-1;
- iy=(j-1)*n+mm-1;
- d=cs[0]*v[ix]+cs[1]*v[iy];
- v[iy]=-cs[1]*v[ix]+cs[0]*v[iy];
- v[ix]=d;
- }
- }
- }
- else
- { kk=ks+1;
- fg[1]=e[kk-2];
- e[kk-2]=0.0;
- for (i=kk; i<=mm; i++)
- { fg[0]=s[i-1];
- sss(fg,cs);
- s[i-1]=fg[0];
- fg[1]=-cs[1]*e[i-1];
- e[i-1]=cs[0]*e[i-1];
- if ((cs[0]!=1.0)||(cs[1]!=0.0))
- for (j=1; j<=m; j++)
- { ix=(j-1)*m+i-1;
- iy=(j-1)*m+kk-2;
- d=cs[0]*u[ix]+cs[1]*u[iy];
- u[iy]=-cs[1]*u[ix]+cs[0]*u[iy];
- u[ix]=d;
- }
- }
- }
- }
- }
- }
-
- free(s);free(e);free(w);
- return(1);
-
-
- }
-
-
- void ppp(float a[],float e[],float s[],float v[],int m,int n)
- { int i,j,p,q;
- float d;
- if (m>=n) i=n;
- else i=m;
- for (j=1; j<=i-1; j++)
- { a[(j-1)*n+j-1]=s[j-1];
- a[(j-1)*n+j]=e[j-1];
- }
- a[(i-1)*n+i-1]=s[i-1];
- if (m<n) a[(i-1)*n+i]=e[i-1];
- for (i=1; i<=n-1; i++)
- for (j=i+1; j<=n; j++)
- { p=(i-1)*n+j-1; q=(j-1)*n+i-1;
- d=v[p]; v[p]=v[q]; v[q]=d;
- }
- return;
- }
-
-
- void sss(float fg[],float cs[])
- { float r,d;
- if ((fabs(fg[0])+fabs(fg[1]))==0.0)
- { cs[0]=1.0; cs[1]=0.0; d=0.0;}
- else
- { d=(float)sqrt(fg[0]*fg[0]+fg[1]*fg[1]);
- if (fabs(fg[0])>fabs(fg[1]))
- { d=(float)fabs(d);
- if (fg[0]<0.0) d=-d;
- }
- if (fabs(fg[1])>=fabs(fg[0]))
- { d=(float)fabs(d);
- if (fg[1]<0.0) d=-d;
- }
- cs[0]=fg[0]/d; cs[1]=fg[1]/d;
- }
- r=1.0;
- if (fabs(fg[0])>fabs(fg[1])) r=cs[1];
- else
- if (cs[0]!=0.0) r=1.0f/cs[0];
- fg[0]=d; fg[1]=r;
- return;
- }
利用VC效果如下:
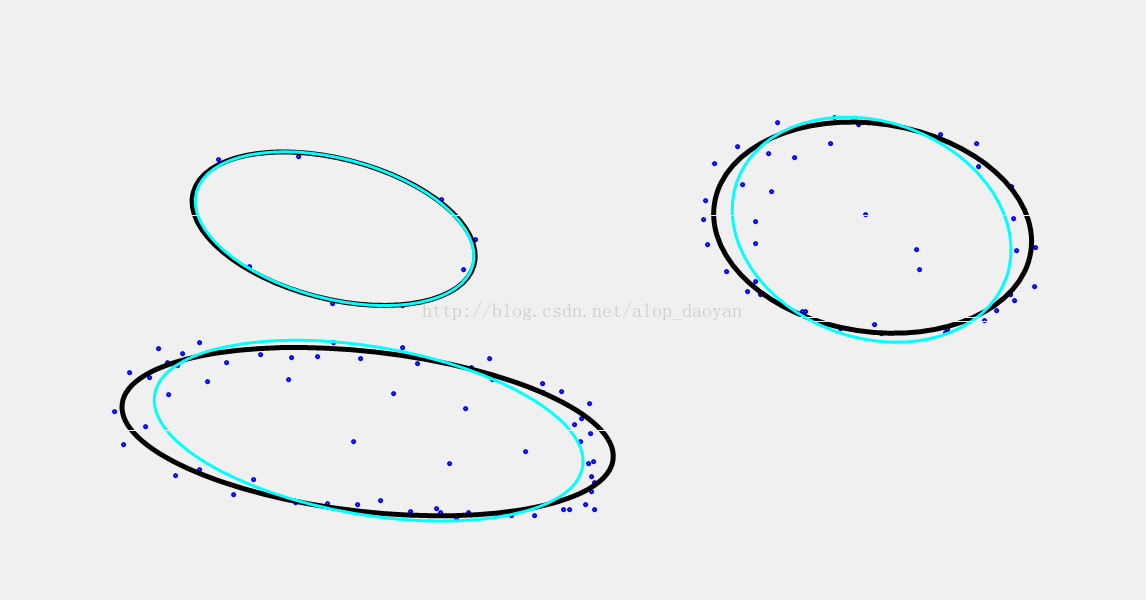
其中青色的线为第一种方法的效果,黑色为第二种方法的拟合效果。
|
 如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】;
如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】; 如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
 如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】;
如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】; 如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
 |申请友链|Archiver|手机版|小黑屋|辽公网安备|晓东CAD家园
( 辽ICP备15016793号 )
|申请友链|Archiver|手机版|小黑屋|辽公网安备|晓东CAD家园
( 辽ICP备15016793号 )