马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?立即注册


×
原文地址: http://www.cnblogs.com/gisoracle/articles/1579529.html
Dijkstra算法求最短路径(C#版)
行如下图的路径,(V0是中心):
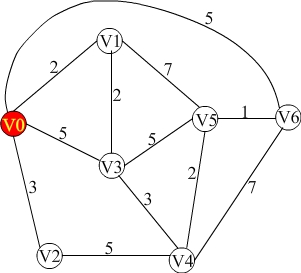
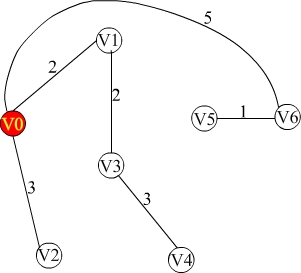
经过该算法后转化为下图
using System;
using System.Collections;
using System.Text; namespace Greedy
{
class Marx
{
private int[] distance;
private int row;
private ArrayList ways = new ArrayList(); public Marx(int n,params int[] d)
{
this.row = n;
distance = new int[row * row];
for (int i = 0; i < row * row; i++)
{
this.distance = d;
}
for (int i = 0; i < this.row; i++) //有row个点,则从中心到各点的路有row-1条
{
ArrayList w = new ArrayList();
int j = 0;
w.Add(j);
ways.Add(w);
}
}
//------------------------------
public void Find_way()
{
ArrayList S = new ArrayList(1);
ArrayList Sr = new ArrayList(1);
int []Indexof_distance=new int[this.row];
for(int i=0; i < row; i++)
{
Indexof_distance=i;
} S.Add( Indexof_distance[0] ); for (int i = 0; i < this.row; i++)
{
Sr.Add( Indexof_distance );
}
Sr.RemoveAt(0);
int[] D = new int[this.row]; //存放中心点到每个点的距离
//---------------以上已经初始化了,S和Sr(里边放的都是点的编号)------------------
int Count = this.row - 1;
while (Count>0)
{
//假定中心点的编号是0的贪吃法求路径
for (int i = 0; i < row; i++)
D = this.distance; int min_num = (int)Sr[0]; //距中心点的最小距离点编号 foreach (int s in Sr)
{
if (D < D[min_num]) min_num = s;
}
//以上可以排序优化
S.Add(min_num);
Sr.Remove(min_num);
//-----------把最新包含进来的点也加到路径中-------------
((ArrayList)ways[min_num]).Add(min_num);
//-----------------------------------------------
foreach (int element in Sr)
{
int position = element * (this.row) + min_num;
bool exchange = false; //有交换标志 if (D[element] < D[min_num] + this.distance[position])
D[element] = D[element];
else
{
D[element] = this.distance[position] + D[min_num];
exchange = true;
}
//修改距离矩阵
this.distance[element] = D[element];
position = element * this.row;
this.distance[position] = D[element]; //修改路径---------------
if (exchange == true)
{
((ArrayList)ways[element]).Clear();
foreach (int point in (ArrayList)ways[min_num])
((ArrayList)ways[element]).Add(point);
}
}
--Count;
}
}
//----------------------------------------------------
public void Display()
{
//------中心到各点的最短路径----------
Console.WriteLine("中心到各点的最短路径如下: \n\n");
int sum_d_index = 0;
foreach(ArrayList mother in ways)
{
foreach (int child in mother)
Console.Write("V{0} -- ", child+1);
Console.WriteLine(" 路径长 {0}",distance[sum_d_index++]);
}
}
} class MainEnterPoint
{
static void Main(string[] args)
{
int r; //列数
Console.Write("请输入点个数(含配送中心点): ");
Int32.TryParse(Console.ReadLine(), out r);
Console.WriteLine("各点分别为: \n");
for (int i = 0; i < r; i++)
Console.Write("V{0} ", i);
Console.Write(" 假定第一个点是配送中心");
Console.WriteLine("\n\n输入各点之间的距离(无通径的用个大整数表示)\n"); int[] a = new int[r * r];
int da; for (int i = 0; i < r; i++)
{
for (int j = i + 1; j < r; j++)
{
Console.Write("V{0} 到 V{1}的距离是: ",i,j);
Int32.TryParse(Console.ReadLine(), out da);
a[i * r + j] = da;
Console.WriteLine();
}
}
//----完善距离矩阵(距离矩阵其实可以是个上三角矩阵,
//----但为了处理方便,还是将其完整成一个对称阵)-----------
for (int i = 0; i < r; i++)
{
for (int j = 0; j < r; j++)
{
if (i == j)
{
a[i * r + j] = 0;
}
a[j * r + i] = a[i * r + j];
}
}
Marx m=new Marx(r,a);
Console.WriteLine();
m.Find_way();
m.Display();
}
}
}
//该程序不但能够算出从中心到各点的最短路径距离,而且把路径也保存了下来.
|  如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】;
如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】; 如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
 如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】;
如果你在论坛求助问题,并且已经从坛友或者管理的回复中解决了问题,请把帖子标题加上【已解决】; 如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
如何回报帮助你解决问题的坛友,一个好办法就是给对方加【D豆】,加分不会扣除自己的积分,做一个热心并受欢迎的人!
 |申请友链|Archiver|手机版|小黑屋|辽公网安备|晓东CAD家园
( 辽ICP备15016793号 )
|申请友链|Archiver|手机版|小黑屋|辽公网安备|晓东CAD家园
( 辽ICP备15016793号 )