基于最小二乘法的平面任意位置椭圆轮廓度误差的精确计算

LoveArx

基于最小二乘法的平面任意位置椭圆轮廓度误差的精确计算

摘要：本文给出一种基于最小二乘原理的椭圆误差精确的计算方法。根据椭圆的性质和特点，计算出各测量点到拟合出的最小二乘椭圆的法向距离从而对椭圆轮廓度进行误差评定，该算法不需进行坐标转换和等间隔测样。文中给出了其数学模型和具体的计算方法。 0 引言 平面曲线轮廓，如渐开线、椭圆和摆线轮廓等在工程中被广泛应用，因此曲线轮廓度测量、识别和误差评定成为轮廓度测量的重要内容[1]。如为了使发动机活塞能与汽缸良好地贴合，提高发动机热能效应，常将活塞截面加工成中凸变椭圆的几何形状[2]。这种中凸变椭圆的活塞裙部形线较为复杂、轮廓加工精度要求较高。因此，研究椭圆轮廓度误差评价方法对保证活塞及其他椭圆轮廓零件的加工质量有重要的意义。 关于椭圆轮廓度误差的评定，国家标准尚未给出明确的定义，也没有给定一种特定的评定算法求解椭圆轮廓度误差。近年来国内外学者开展这方面的研究较少，取得了一些研究成果。比较有代表性的成果有刘书桂等[3]基于最小二乘原理的椭圆误差的评价方法。邹益民等[4]基于几何距离的拟合算法。侯宇等[5]采用有效集法进行数据处理。陈基伟[6]提出的椭圆直接拟合算法。t.s.r.murthy[7]提出的正交最小二乘法、二项高斯分布法和基于代数距离的最小二乘法来评定椭圆轮廓度误差。这些评定方法对于椭圆误差的评定都有一定的作用和效果。 本文通过平面任意位置椭圆方程、椭圆法线方程特点和椭圆本身性质，利用最小二乘原理实现对平面任意位置椭圆轮廓度误差的评定。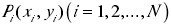 1 最小二乘椭圆拟合 设平面任意位置椭圆(如图1所示)方程为： 设 为椭圆轮廓上的n(n≥5)个测量点，依据最小二乘原理，所拟合的目标函数为： 欲使f为最小，须使 由此可得正规方程： 解方程(3)可得到a, b ,c , d和e的值，由参考文献[3]可得到拟合出的最小二乘椭圆的五个主参数：位置参数(θ, x , y)及形状参数(a , b )。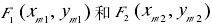 2 确定过测量点的椭圆法线与最小二乘椭圆的交点 如图1所示，设点mi(xi、yi)为过测量点pi(xi、yi)的椭圆法线与最小二乘椭圆的交点，由于交点mi(xi、yi)既在法线上又在最小二乘椭圆[9]上，即点m(xi、yi)满足方程组： 3 判断各测量点ip的位置 设拟合出的最小二乘椭圆的两个焦点为 (如图1所示)。依据椭圆的性质可得： 测量点pi点到两焦点的距离之和ddi为： 圆弧上的速度v=4.995。 与求在可行路径1p上的最短时间一样，可求得在可行路径2p上的最短时间是t=96.56322秒。 所以从o→a的最短时间t=min{t1,t2}=94.228312秒，最短时间路径如上所述。 4 结束语 由于机器人在圆弧上的移动速度随圆弧半径的增大而增大，所以机器人从起点到终点的最短路径并非最短时间路径;从o→a可看出，移动距离是半径的增函数;当r<r0=12.4时移动时间是半径的减函数，当r>r0=12.4时移动时间是半径的增函数，r=12.40是移动时间的极小值点;所以在从起点到终点路径的选择上，应在距离和时间上作权衡，做出决策。 参考文献： [1] 金秀慧,伊连云.基于通用运动学模型的移动机器人避障路径规划[j].机械工程师,2005,12. [2] 罗熊,樊晓平.具有大量不规则障碍物的环境下机器人路径规划的一种新型遗传算法x,机器人robot,2004. [3] 席志红,原新.基于视觉的移动机器人实时避障和导航哈尔滨工程[j],大学学报,2002. [4] 赵静,但琦.数学建模与数学实验[m].高等教育出版社2010. [5] 任善强.数学模型(第二版)[m].重庆大学出版社,1993. [6] 王学辉.matlab6.1[m].中国水利水电出版社.2002. 收稿日期：2012-10-26 基金项目：河南省基础与前沿技术研究计划项目(122300410114) 作者简介：崔静伟(1986-)，女，硕士研究生，研究方向为精密测试技术。